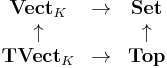Category of topological vector spaces
In mathematics, the category of topological vector spaces is the category whose objects are topological vector spaces and whose morphisms are continuous linear maps between them. This is a category because the composition of two continuous linear maps is again continuous. The category is often denoted TVect or TVS.
Fixing a topological field K, one can also consider the (sub-)category TVectK of topological vector spaces over K with continuous K-linear maps as the morphisms.
TVect is a concrete category
Like many categories, the category TVect is a concrete category, meaning its objects are sets with additional structure (i.e. a vector space structure and a topology) and its morphisms are functions preserving this structure. There are obvious forgetful functors into the category of topological spaces, the category of vector spaces and the category of sets.
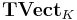 is a topological category
is a topological category
The category is topological, which means loosely speaken that it relates to its "underlying category" the category of vector spaces in the same way that Top relates to Set. Formally: For every single K-vector space  and every family
and every family 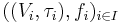 of topological K-vector spaces
of topological K-vector spaces 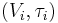 and K-linear maps
and K-linear maps 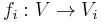 , there exists a vector space topology
, there exists a vector space topology  on
on  so that the following property is fulfilled:
so that the following property is fulfilled:
Whenever 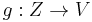 is a K-linear map from a topological K-vector space
is a K-linear map from a topological K-vector space 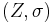 it holds:
it holds:
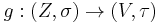 is continuous
is continuous 
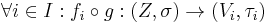 is continuous.
is continuous.
The topological vector space 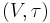 is called "initial object" or "initial structure" with respect to the given data.
is called "initial object" or "initial structure" with respect to the given data.
If one replaces "vector space" by "set" and "linear map" by "map", one gets a characterisation of the usual initial topologies in Top. This is the reason why categories with this property are called "topological".
There are numerous consequences of this property. For example:
- "Discrete" and "indiscrete" objects exist. A topological vector space is indiscrete iff it is the initial structure with respect to the empty family. A topological vector space is discrete iff it is the initial structur with respect to the family of all possible linear maps into all topological vector spaces. (This family is a proper class, but in fact that doesn't matter: Initial structures with respect to all classes exists iff they exists with respect to all sets)
- Final structures (the similar defined analogue to final topologies) exist. But there is a catch: While the initial structure of the above property is in fact the usual initial topology on
 with respect to
with respect to 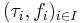 , the final structures don't need to be final with respect to given maps in the sense of Top. For example: The discrete objects (=final with respect to the empty family) in
, the final structures don't need to be final with respect to given maps in the sense of Top. For example: The discrete objects (=final with respect to the empty family) in 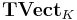 do not carry the discrete topology.
do not carry the discrete topology. - Since the following diagram of forgetful functors commutes
-
- and the forgetful functor from
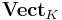 to Set is right adjoint, the forgetful functor from
to Set is right adjoint, the forgetful functor from 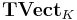 to Top is right adjoint too (and the correspondig left adjoints fit in an analogue commutative diagram). This left adjoint defines "free topological vector spaces". Explicitly these are free K-vector spaces equipped with a certain initial topology.
to Top is right adjoint too (and the correspondig left adjoints fit in an analogue commutative diagram). This left adjoint defines "free topological vector spaces". Explicitly these are free K-vector spaces equipped with a certain initial topology.
- Since
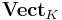 is (co)complete,
is (co)complete, 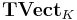 is (co)complete too.
is (co)complete too.
References
- Lang, Serge (1972). Differential manifolds. Reading, Mass.–London–Don Mills, Ont.: Addison-Wesley Publishing Co., Inc..